In-solution Biophysics

FIDA: Flow Induced Dispersion Analysis
I'm Interested

FIDA technology embodies first-principles thinking.

It uses first principles of physics and fluid mechanics to analyze the movement of particles in a fluid.
Thanks to its simplicity, it can deliver a wealth of data, with just one assay.

1. Laminar Flow

Laminar flow is a smooth, non-turbulent flow of a fluid pushed through a capillary. In a laminar flow regime, the fluid moves in parallel streams.

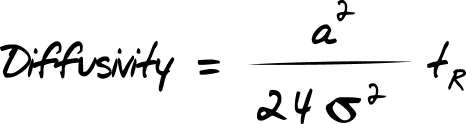
2. Taylor Dispersion

Taylor dispersion describes the behaviour of small particles in the flow. As the flow is laminar, the particles will not mix evenly, but instead experience a fluctuating motion. Such a motion results in a dispersion of the particles over time and space, as they diffuse and move along the flow.

FIDA technology takes advantage of these two principles

by measuring fluorescence of particles in the laminar flow and analysing their dispersion over time, which allows for calculation of the hydrodynamic radius of a particle of interest.

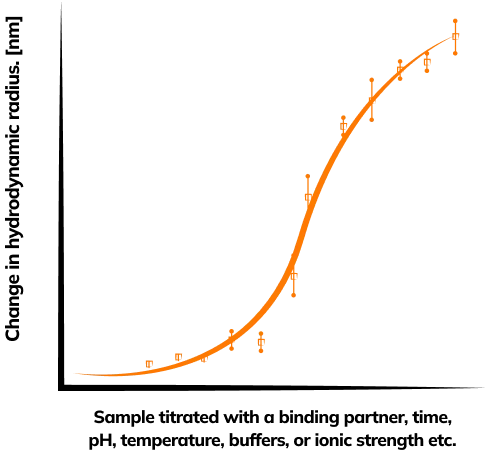
Additionally, hydrodynamic radius measurement opens door to another crucial biophysical property: the binding between two or more biomolecules

As biomolecules come together and bind in solution, their diffusivity (D) decreases; that is, the bound molecules will diffuse slower through the capillary and generate a more extended dispersion profile and diffusion coefficient (D). Using the Stokes-Einstein equation, FIDA software reveals the increase in size (Rh) of the molecules as they bind together. Titrating your molecule of interest with its binding partners in a simple FIDA experiment uncovers a wide range of binding parameters, such as affinity (Kd), derived directly from the hydrodynamic radius and the Stokes-Einstein equation.

Would you like to dive into details? Here’s how it works:

If anything remains unclear, feel free to reach out
Ask a question to our scientist
Step

01

The sample of interest is passed through a thin capillary. Due to the difference in velocity between the walls and center of the capillary, the sample shapes into a parabolic profile.

Step

02

Molecules diffuse radially, away from the flow axis. The fluorescence emitted by the molecules is acquired as a Gaussian signal by a high sensitivity detection system and is plotted against time.

Step

03

The size of the molecules in the sample determines their radial diffusivity, which in turn defines the extent of sample’s dispersion.

Small molecules diffuse faster and create a more compact dispersion profile. Large molecules diffuse slower, which results in a more extended dispersion profile.

Step

04

This enables FIDA to detect size changes smaller than 5%. The math behind the software calculations is based on Taylor dispersion phenomena and the Stokes-Einstein equation, which provide a firm base for further calculations.

How do FIDA users benefit from the first principles?

Accuracy

Since FIDA is not dependent on a priori assumption or on empirical calibration, it ensures accuracy and provides flexibility in analysing diverse samples.

Data Transparency

On top of that, having direct measurements translates into high data transparency, necessary for quality control or even machine learning.

Certainty

Finally, the chance that your measurements do not reflect reality, are imprecise, or are a false positive/negative is much lower in first principle technologies. To be frank, we think that first principle technologies are the future.
Discovery Call

Watch the video for more!

Pilot your samples
Book a discovery call